Закон радиоактивного распада

Закон радиоактивного распада.

Фредерик Содди и Эрнест Резерфорд первыми экспериментально обнаружили, что скорость распада радиоактивного изотопа пропорциональна его количеству в текущий момент:

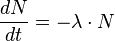$\frac{dN}{dt}= -\lambda \cdot N$ (1)

Знак минус отражает уменьшение количества радиоактивного нуклида со временем, а коэффициент пропорциональности λ характеризует скорость его распада. Перегруппируем выражение (1):

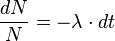
$\frac{dN}{N}= -\lambda \cdot dt$

В результате интегрирования находим:

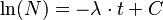$\ln(N)= -\lambda \cdot t + C$ (2)

Постоянная интегрирования C легко определяется при t=0 :

$C = ln(N 0)$ - это начальное количество нуклида. Теперь уравнение (2) выглядит так:

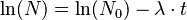$\ln(N)= \ln(N_0) - \lambda \cdot t$ , откуда легко находим связь между оставшимся и исходным количеством радиоактивного нуклида:

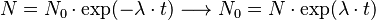$N= N_0 \cdot \exp(- \lambda \cdot t) \longrightarrow N_0= N \cdot \exp( \lambda \cdot t)$ (3)

Количество дочернего, радиогенного изотопа D_rad находим из очевидного равенства:

$D r a d = N 0 - N$ . Подставляя сюда N₀ из уравнения (3), находим:

$D_{rad}= N \cdot [ \exp( \lambda \cdot t) - 1]$ . (4)

Это уравнение можно разрешить относительно t :

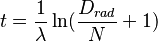$t = \frac{1}{ \lambda} \ln( \frac{D_{rad}}{N} +1)$ . (5)

Таким образом из измеренных атомных количеств накопленного дочернего изотопа (D_rad) и оставшегося материнского (N) можно вычислить время, за которое накопился радиогенный изотоп. Уравнения (3), (4) и (5) представляют собой разные алгебраические формы закона радиоактивного распада.